pythonで軌道シミュレーション
目次
画像書き出し

# Import Python Modules import numpy as np # 数値計算ライブラリ import matplotlib.pyplot as plt # 描画ライブラリ from scipy.integrate import odeint # 常微分方程式を解くライブラリ # 定数 # G = 6.67430 * 10 **(-20) [km^3 kg^-1 s^-2] 万有引力定数(km) # M = 5.972 * 10 ** 24 # [kg] 地球質量 GM = 398600 # [km^3 s^-2] 地球の重力定数 # 二体問題の運動方程式 def func(x, t): r_E = np.linalg.norm([x[0],x[1],x[2]]) dxdt = [x[3], x[4], x[5], -GM*x[0]/(r_E**3), -GM*x[1]/(r_E**3), -GM*x[2]/(r_E**3)] return dxdt # 微分方程式の初期条件 x0 = [6400, 0, 0, 0, 9, 0] # 位置(x,y,z)+速度(vx,vy,vz) t = np.linspace(0, 30000, 1000) # (開始、終了、ステップ数) 1日分 軌道伝播 # 微分方程式の数値計算 sol = odeint(func, x0, t) # 二次元描画 fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.set_xlabel('km') ax.set_ylabel('km') #地球をプロット ax.plot(0,0,'.', c='black') #点をプロットする場合 ax.plot(sol[:, 0],sol[:, 1], 'black') #numpyのnparrayの記法で、各時間の0列目(x座標)、1列目(y座標)を抽出 ax.set_aspect('equal') # グラフのアスペクト比を揃える plt.savefig('orbit.png') # 画像を保存 plt.show()
kmで計算しているので、万有引力定数が-11乗でなく-20乗になっている。万有引力を万有引力定数Gと地球質量Mから計算すると誤差が大きくなるため、重力定数GMとしてハードコードしている
地球の大きさを描画する

# Import Python Modules import numpy as np # 数値計算ライブラリ import matplotlib.pyplot as plt # 描画ライブラリ from scipy.integrate import odeint # 常微分方程式を解くライブラリ from matplotlib import patches # 定数 # G = 6.67430 * 10 **(-20) [km^3 kg^-1 s^-2] 万有引力定数(km) # M = 5.972 * 10 ** 24 # [kg] 地球質量 GM = 398600 # [km^3 s^-2] 地球の重力定数 R = 6378 # 二体問題の運動方程式 def func(x, t): r_E = np.linalg.norm([x[0],x[1],x[2]]) dxdt = [x[3], x[4], x[5], -GM*x[0]/(r_E**3), -GM*x[1]/(r_E**3), -GM*x[2]/(r_E**3)] return dxdt # 微分方程式の初期条件 x0 = [R+600, 0, 0, 0, 9, 0] # 位置(x,y,z)+速度(vx,vy,vz) t = np.linspace(0, 30000, 1000) # (開始、終了、ステップ数) 1日分 軌道伝播 # 微分方程式の数値計算 sol = odeint(func, x0, t) # 二次元描画 fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.set_xlabel('km') ax.set_ylabel('km') #地球をプロット c = patches.Circle( (0,0), R) ax.add_patch(c) # ax.plot(0,0,'.') #点をプロットする場合 ax.plot(sol[:, 0],sol[:, 1], 'black') #numpyのnparrayの記法で、各時間の0列目(x座標)、1列目(y座標)を抽出 ax.set_aspect('equal') # グラフのアスペクト比を揃える plt.savefig('orbit.png') # 画像を保存 plt.show()
マウスを使って三次元で観察する

# Import Python Modules import numpy as np # 数値計算ライブラリ import matplotlib.pyplot as plt # 描画ライブラリ from scipy.integrate import odeint # 常微分方程式を解くライブラリ # 定数 # G = 6.67430 * 10 **(-20) [km^3 kg^-1 s^-2] 万有引力定数(km) # M = 5.972 * 10 ** 24 # [kg] 地球質量 GM = 398600 # [km^3 s^-2] 地球の重力定数 # 二体問題の運動方程式 def func(x, t): r_E = np.linalg.norm([x[0],x[1],x[2]]) dxdt = [x[3], x[4], x[5], -GM*x[0]/(r_E**3), -GM*x[1]/(r_E**3), -GM*x[2]/(r_E**3)] return dxdt # 微分方程式の初期条件 x0 = [6000, 0, 0, 0, 8, 1] # 位置(x,y,z)+速度(vx,vy,vz) t = np.linspace(0, 30000, 1000) # (開始、終了、ステップ数) 1日分 軌道伝播 # 微分方程式の数値計算 sol = odeint(func, x0, t) # 三次元描画 fig = plt.figure() ax = fig.add_subplot(1, 1, 1, projection='3d') ax.plot(0,0,0,'.')#地球をプロット ax.plot(sol[:, 0], sol[:, 1], sol[:, 2],linewidth = 0.5) ax.set_aspect('equal') # グラフのアスペクト比を揃える plt.show()
初速のz成分を0km/sから1km/sに変更し、三次元でプロットした
gif動画を書き出す
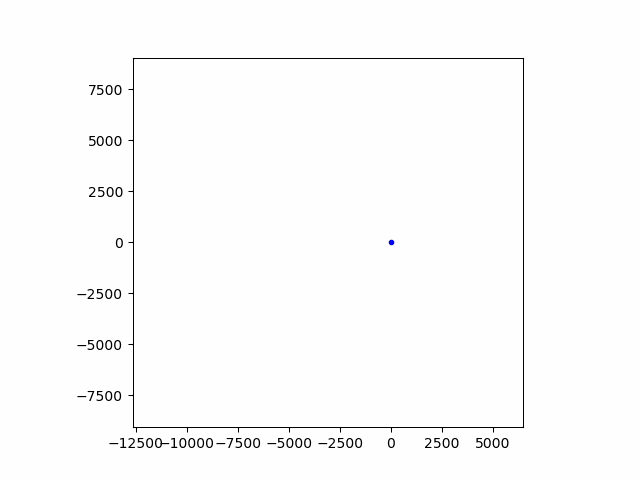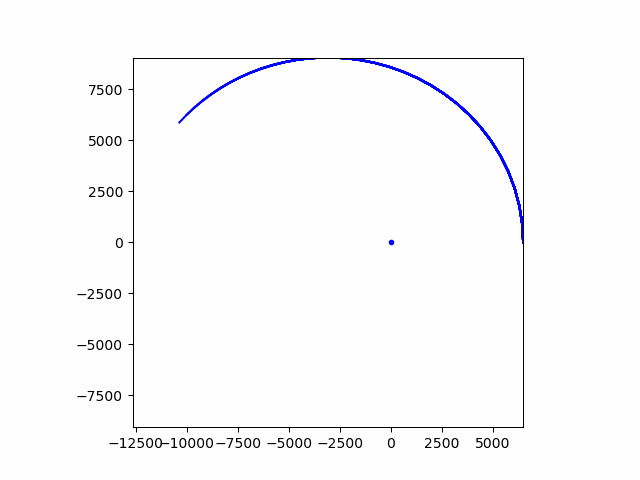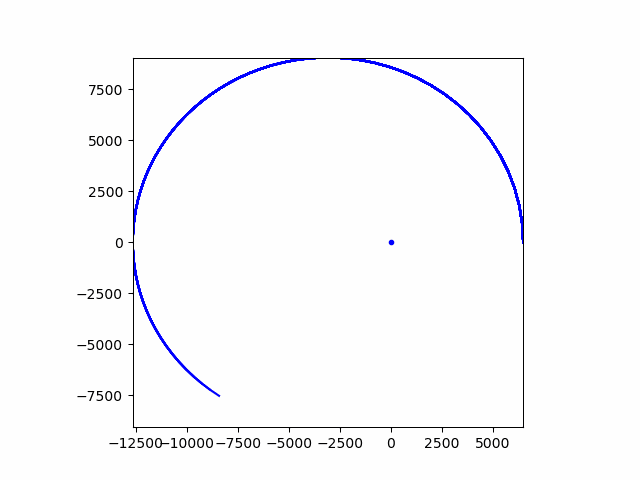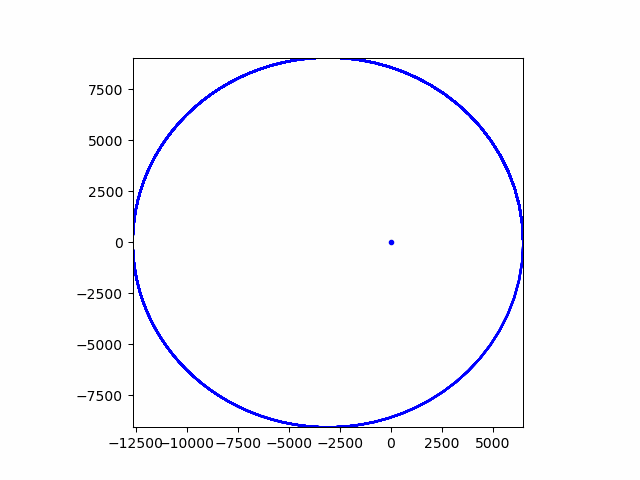
import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation from scipy.integrate import odeint # 常微分方程式を解くライブラリ GM_E = 398600 # km3/s2 地球の重力定数 L_E = [0,0,0] def func(x, t): r_E = np.linalg.norm([x[0]-L_E[0],x[1]-L_E[1],x[2]-L_E[2]]) dxdt = [x[3], x[4], x[5], -GM_E*x[0]/(r_E**3), -GM_E*x[1]/(r_E**3), -GM_E*x[2]/(r_E**3)] return dxdt def update(i, x, y): plt.plot(x[0:i], y[0:i],c="blue") def draw(): # 微分方程式の初期条件 r0 = [6500, 0, 0, 0, 9, 0] # 位置(x,y,z)+速度(vx,vy,vz) t = np.linspace(0, 10000, 1000) # 1日分 軌道伝播 sol = odeint(func, r0, t) print("keisan owari") # 抽出して二次元化 x1, y1, z1 = sol[:, 0], sol[:, 1], sol[:, 2] x = x1[::10] y = y1[::10] fig = plt.figure() #figure objectを取得 plt.plot(0,0,'.',c='blue')# 地球をプロット plt.xlim(min(x),max(x)) plt.ylim(min(y),max(y)) plt.gca().set_aspect('equal') ani = animation.FuncAnimation(fig, update, fargs = (x, y), frames = len(x),interval = 10) ani.save("orbit.gif", writer = 'pillow',fps=30) draw()
mp4を書き出す
mp4を書き出す場合は、writerをpillowから次のように変える
ani = animation.FuncAnimation(fig, update, fargs = (x, y), frames = len(x),interval = 10) writer = animation.writers['ffmpeg'](fps=60, metadata=dict(artist='mika'), bitrate=200) ani.save("orbit.mp4", writer = writer)
月と、太陽の摂動と、太陽地球回転フレーム
import numpy as np import matplotlib.pyplot as plt import matplotlib.animation as animation from scipy.integrate import odeint # 常微分方程式を解くライブラリ import glob # G = 6.67430 * 10 **(-11) [m3 kg-1 s-2] 万有引力定数(mksa) # G = 6.67430 * 10 **(-20) [km3 kg-1 s-2] 万有引力定数(km) # ME = 5.972 * 10 ** 24 # [kg] 地球質量 # MM = 7.345 * 10 ** 22 # [kg] 月質量 MS = 1.989 * 10 ** 30 # [kg] 太陽質量 GM_E = 398600.4354360959 # [km3 s-2] 地球の重力定数 GM_M = 4902.8072 # [km3/s2] 月の重力定数 GM_S = 13.27 * 10 ** 10 # [km3 s-2] 太陽の重力定数 L_E = [0,0,0] # 地球の座標[km] # R_SE = 1.496 * 10 ** 8 # [km] 地球公転半径 R_EM = 3.8 * 10 ** 5 # [km] 月公転半径 # A = 5.927 * 10 ** -6 # [km s-2] 地球付近での太陽重力の加速度 # GM_S/R_SE W = 2*np.pi/(86400*365) w = 2*np.pi/(86400*30) gradA = 17.74 * 10 ** (-14) # GM_S/R_SE ** 3 # [km s-2] 地球付近での太陽重力と遠心力による加速度の傾斜 GM_S/R_SE**2 + W**2 def L_M(t): # 月の運動 offset = 170/360 * 2*np.pi return [-384400*np.cos(w*t+offset),-384400*np.sin(w*t+offset),0] def F(r, t): r_E = np.linalg.norm([r[0]-L_E[0],r[1]-L_E[1],r[2]-L_E[2]]) r_M = np.linalg.norm([r[0]-L_M(t)[0],r[1]-L_M(t)[1],r[2]-L_M(t)[2]]) LM = L_M(t) dxdt = [r[3], r[4], r[5], GM_E*(L_E[0]-r[0])/(r_E**3) + GM_M*(LM[0]-r[0])/(r_M**3) + gradA * r[0] * np.cos(W*t), GM_E*(L_E[1]-r[1])/(r_E**3) + GM_M*(LM[1]-r[1])/(r_M**3) + gradA * r[1] * np.sin(W*t), GM_E*(L_E[2]-r[2])/(r_E**3) + GM_M*(LM[2]-r[2])/(r_M**3)] return dxdt def update(i, x, y, unittime,framew): t = i*unittime LM = L_M(t) plt.cla() #現在描写されているグラフを消去 plt.plot(0,0,0,'.',c='blue')# 地球をプロット plt.plot(LM[0]*np.cos(framew*t)+LM[1]*np.sin(framew*t), -LM[0]*np.sin(framew*t)+LM[1]*np.cos(framew*t), '.',c='red')# 月をプロット plt.xlim(-2000000,1500000) plt.ylim(-1500000,1500000) plt.plot(x[0:i], y[0:i],c="blue") #plot plt.text(-1500000,-1000000,f'day = {int(t/86400)}', fontsize=10) def draw(): # 微分方程式の初期条件r0 v0 = 11.48964 #初速12.5922 12.592 h0 = 6000 # 初期高度 th0 = np.pi*1 # 初期位置の経度(太陽側が0、反時計回り) r0 = [-h0*np.cos(th0), -h0*np.sin(th0), 0, v0*np.sin(th0), -v0*np.cos(th0), 0] # 位置[km](x,y,z)+速度[km/s](vx,vy,vz) # 微分方程式の計算設定 timeRange = int(86400 * 320) #時間範囲[s] (参考 1d=86400s) calcStep = 40 #時間ステップ[s] t = np.linspace(0, timeRange, int(timeRange/calcStep)) # 時間範囲(開始[s],終了[s],分割数) # 微分方程式を解く sol = odeint(F, r0, t) # [x, y, z, u, v, w] # print(sol[5]) x1 = [] y1 = [] z1 = [] framew = W for i, raw in enumerate(sol): t = i*calcStep x1.append(raw[0]*np.cos(framew*t) + raw[1]*np.sin(framew*t)) y1.append(-raw[0]*np.sin(framew*t) + raw[1]*np.cos(framew*t)) z1.append(raw[2]) # 動画保存用にフレームを抜き出す skiprate = int(1440/calcStep*15) #144skiprateで、60fps 10秒step計算で1秒が一日になる x = x1[::skiprate] y = y1[::skiprate] dic = calcStep*skiprate fig = plt.figure() #figure objectを取得 plt.gca().set_aspect('equal') ani = animation.FuncAnimation(fig, update, fargs = (x, y,dic,framew), frames = len(x),interval = 10) # savemp4(ani,'ww.mp4') savegif(ani,'16.gif') # savemp4(ani,getname()) def getname(): filelist = [int(filename.split('.')[0].replace('test','')) for filename in glob.glob('*.mp4')] return f'test{max(filelist)+1}.mp4' def savemp4(ani,filename): writer = animation.writers['ffmpeg'](fps=60, metadata=dict(artist='mika'), bitrate=200) ani.save(filename, writer = writer) def savegif(ani,filename): ani.save(filename, writer = 'pillow', fps=30) draw()